커뮤니티2
데이터 엔지니어링데이터 엔지니어링
[ML/DL] Transformer - Relative Positional Embedding
Vaswani의 트렌스포머 아키텍처와 비슷하지만 이번 Shaw et al의 Self-Attention with Relative Position Representations(https://arxiv.org/abs/1803.02155)는 기존의 아키텍처에서 조금의 변경사항이 있다.
가장 큰 변경사항은 Positional Encoding대신에 사용된 Relative Positional Embedding의 사용과 함께 기존의 Self-Attention 메카니즘의 연산에서의 추가 사항이 있다.
이번글에서는 Vaswani의 아키텍처에서의 Self-Attention 연산과의 차이점과 Relative Positional Embedding에 대해서 설명해보려 한다.
우선 기존 트렌스포머는 Token Embedding과 Positional Encoding의 합을 Self-Attention에 적용한다.
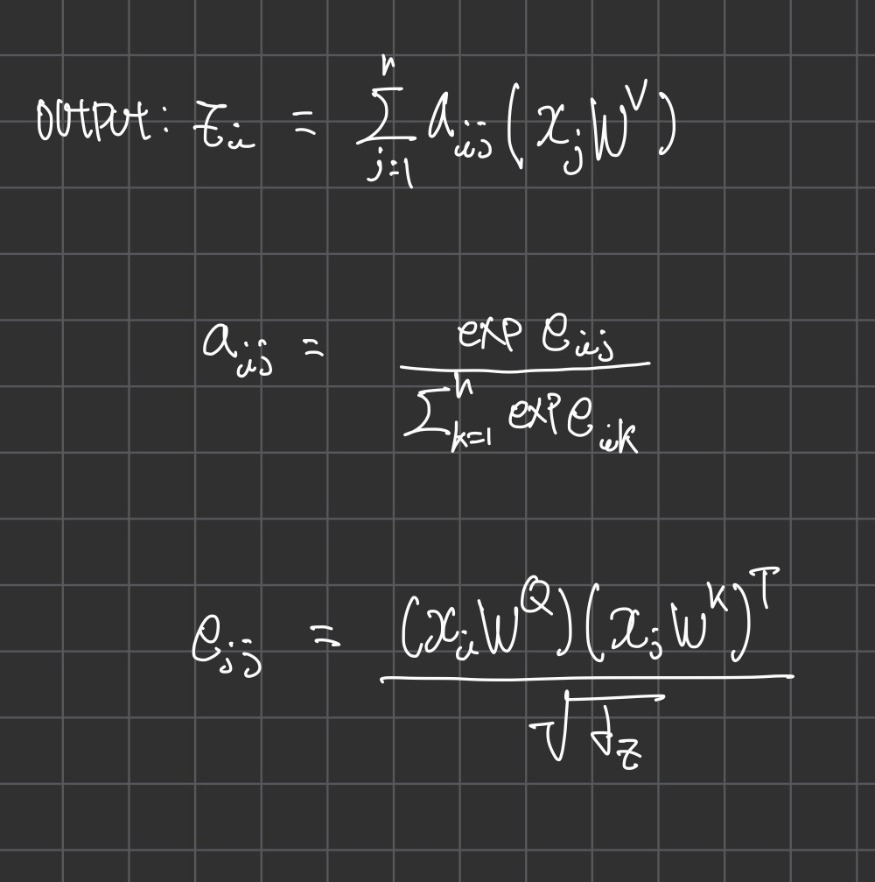
위의 수식에서 z는 self-attention의 결과이며, 아래 수식은 Scaled Dot-Product Attention을 통한 Attention Score를 구하는 방법이다. 자세한 설명은 Vaswani의 Attention is all you Need에서 찾아볼수 있다.
다음은 Relative Positional Representation에서의 Positional Embedding을 함께 사용하여 연산하는 Self Attention이다.
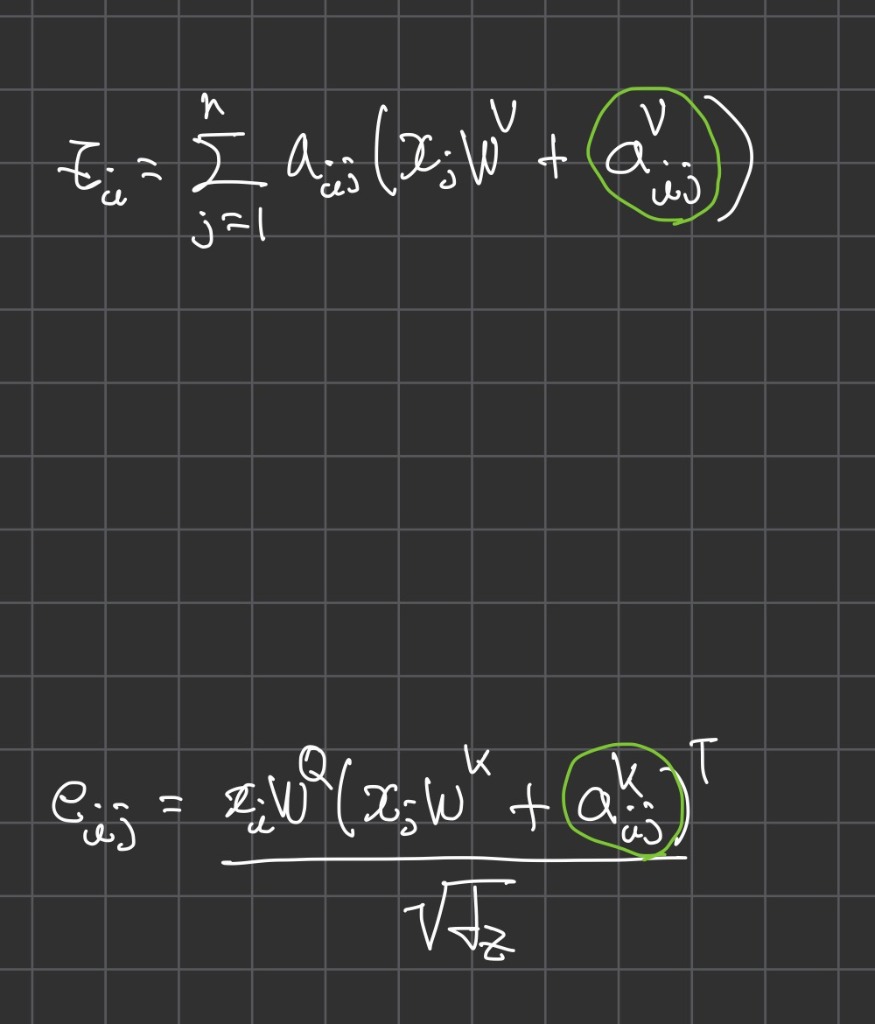
e_ij와 z_i를 구할때 2개의 Relative Positional Embedding을 추가하여 Self Attention을 적용하였다.
위의 수식에서 e_ij를 구할때 추가된 (a_ij^k)와 z_i를 구할때 추가된 (a_ij^v) 2개의 요소가 Positional Embedding이다.
e_ij를 구한이후 Vaswani의 수식에서 a_ij를 구하는것은 동일하다.
그렇다면, 이 논문에서 얘기하는 Relative Position이란 무엇인가?
예를 들어서
5단어로 이루어진 어떠한 문장이 있다고 가정하고, 이를 토큰화를 진행하였다.
그랬을때 우리는, [A, B, C, D, E]라는 순서를 가진 Input을 가졌다고 가정하였을때,
각 단어들의 거리 (Distance)를 통하여 Relative Postional Representation (RPR)을 구한다고 한다.
위의 예시에서
A는 B, C, D, E 의 거리
B는 A, C, D, E 의 거리를 구하며, 자기 자신의 거리또한 구한다.
여기서 중요한점은 C를 기준으로 A,B,D,E와의 거리를 구할때 A,B는 C의 앞에, D와 E는 C의 뒤에 나왔는데,
이러한 순서도 중요하게 보아야 한다.
따라서 5개의 단어에 대해서 나타낼수 있는 거리는
앞으로 4단어, 뒤로 4단어, 자기 자신인 총 9개의 거리를 구할수 있다.
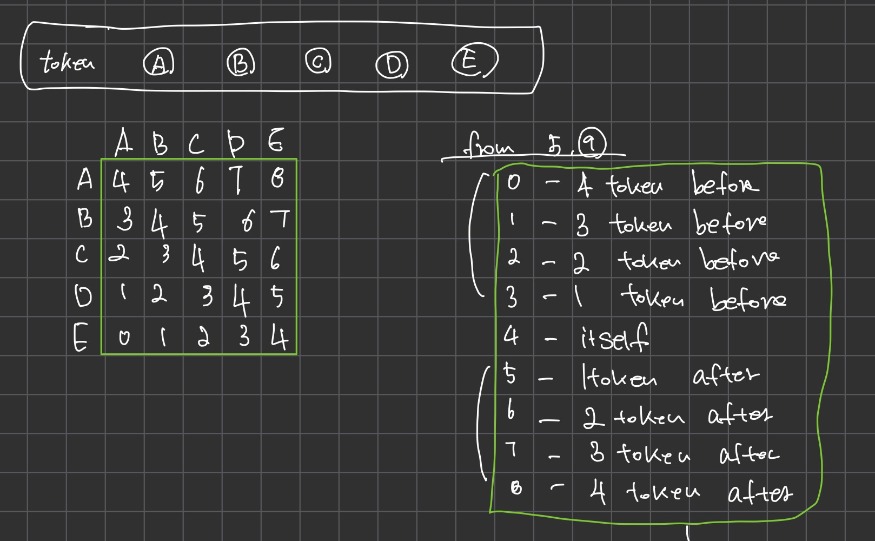
총 9개의 거리에서
0은 기준이 되는 단어에서 4단어 앞에,
1은 3단어 앞에
2는 2단어 앞에
3은 1단어 앞에
4는 자기 자신으로,
5는 1단어 뒤에
6은 2단어 뒤에
7은 3단어 뒤에
8은 4단어 뒤에
이런 경우의 수가 나타난다.
오른쪽은 0부터 8까지의 인덱스에 대한 설명이며, 왼쪽에 있는 행렬이 "Distance Matirx"라고 한다.
논문에서는 최대 몇 단어까지 RPR을 볼것인지 규정하는 K라는 변수가 있다.
보편적인 NLP의 학습시에는 문장의 길이가 위의 예시랑은 다르게 꽤 길기 때문에 이에 대한 고찰이 있었는데, 논문상에서는 꽤나 큰 차이를 보여주지 않은것 같다.

구현을 하며 Shaw et al 의 RPR에 대해 심층적으로 이해해 보자면,
우선 가상의 데이터와 파라미터를 설정해보자.
간단한 구현을 위해서,
Batch Size = 2
Sequence Length = 5
Embedding Dimension = 12
논문의 k = 5
따라서 Input의 크기는 [b, s, d] 인 [2, 5, 12]의 크기를 가지는 텐서이다.
[1] 학습에 따라 값이 변하는 Parameter를 초기화 해준다.
해당 파라미터는 학습에 진행되는 {2*최대 단어길이 + 1}이며, 5개의 단어를 정해놓았다면,
11개로, 이는 논문에서 얘기하는 2k+1을 따랐다.


초기화된 파라미터는 (2s+1, d)의 크기를 가진다 [11, 12]
[2] Distance Matrix를 생성한다.
행벡터와 열벡터의 연산으로 Distance Matrix를 구할수 있다.
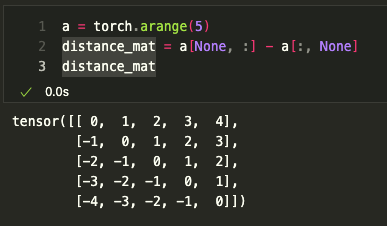
이후 논문 3.2에서 얘기한 clip(x, k)를 진행한다.
만약 K가 4보다 작다면, 4보다 큰 값은 최대 값으로 고정된다.
예를 들면
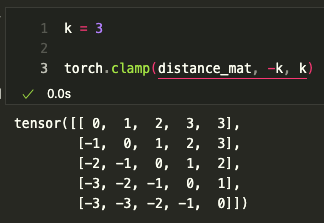
k를 3으로 하였을때 -4, 4는 사라지고, 3과 -3으로 변경되었다
[3] Clamp된 Distance Matrix를 구했다면, 해당 값을 음수가 아닌 양수로 바꿔준다.
따라서 Distance Matrix에 K를 더해준다.
아래 예제에서는 k=5를 사용한것을 기본으로 한다
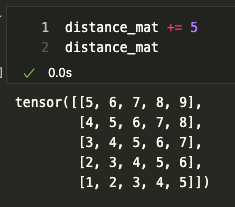
[4] Distance Matrix는 거리에 따른 임베딩값의 Index에 대한 값을 가진 행렬임으로,
[1]에서 초기화 하였던 Embedding Table에서 Distance Matrix의 인덱스에 해당하는 임베딩을 가져온다.

[5] Positional Embedding을 추출했다면, 논문에서 제안한 e_ij에 대한 연산을 진행해보자.

xW{Q}는 [b, s, d]의 크기를 가진 텐서이고,
xW{K}도 [b, s, d]의 크기를 가졌다.
두 텐서의 Dot Product를 위해 xW{K}의 Transpose를 진행하면 [b, s, s]의 크기를 가진 텐서가 나온다.
xW{Q}와 Embedding의 연산은 바로 되지 않기에
xW{Q}[b, s, d]와 Embedding [s, s, d]를 조금 변경해준다.
xW{Q}는 [b, s, 1, d]로 변경해주고, Embedding은 Transpose를 취해준다 [s, d, s]
두 텐서의 Dot Product는 [b, s, 1, s]로 나타나고, 추가했던 2번째 디멘션을 제거한다.

예시를 위해 wq와 emb는 random값으로 초기화 하여 연산의 가능성만 확인하였다.
아래 구현에서는 MultiHead를 포함한 구현 예시이다.
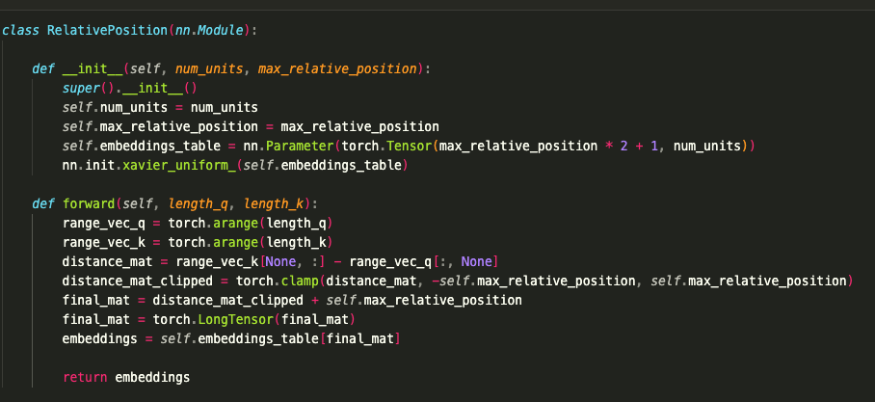
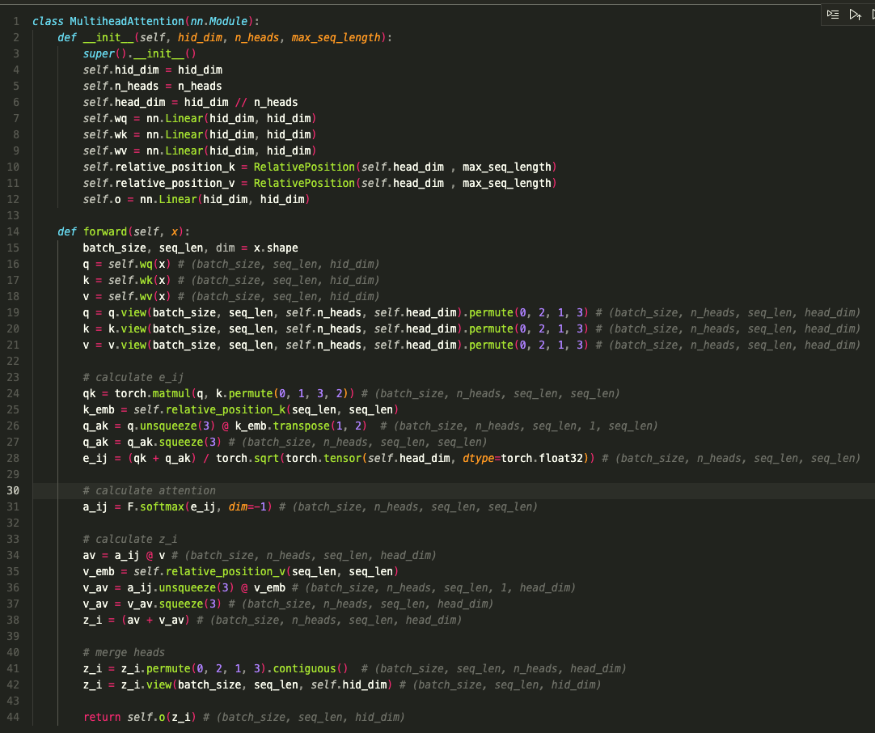
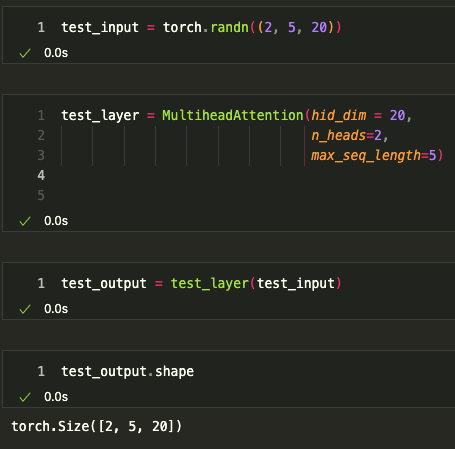
다른 구현은 여기에서 볼수 있다.
https://github.com/evelinehong/Transformer_Relative_Position_PyTorch/blob/master/relative_position.py
이렇게 해서 Relative Postional Embedding을 통한 Multi Head Attention을 사용할수 있다.
그러나, 2018 12월에 Huang의 논문에서 이러한 방식의 구현이 GPU 메모리에 과도한 점유율을 보여주는점을 시작으로, RPR을 개선하는 논문을 발표했다.
Shaw의 논문은 2018 4월에 발표되었고, Huang의 논문은 2018 12월에 발표 되었다.
Music Transformer (https://arxiv.org/abs/1809.04281)

Huang은 Skewing Mechanism으로 GPU 메모리를 더 효율적으로 사용하는 Relative Positional Attention을 소개하였다. 가장 중요한 핵심은, Distance Matrix에서 임베딩을 가져오는 부분이다.
우선 위에서 했듯이 우리는 (2s+1, d)의 임베딩 테이블을 초기화 했으나, 정작 사용하는 임베딩은 (2s-1)개 이다.
5개의 단어로 예를 들면 앞으로 4개, 뒤로 4개, 자신 1개 (총 9개)를 사용한다.
따라서 임베딩 테이블을 (2s-1, d)로 초기화를 해준다.

그 다음, scaled dot product연산을 진행한다.
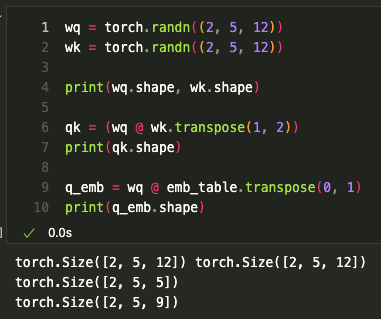
q_emb는 [b, s, 2s-1]의 값을 가지고 있다.
예시의 값은 [2, 5, 9]이며,
모든 RPR을 생각해보면, 아래 그림을 그려볼수 있다.

왼쪽의 테이블처럼, 첫번째 단어는 [4,5,6,7,8]의 인덱스,
두번째 단어는 [3,4,5,6,7]의 인덱스를 가진다.
조금더 크게 확장해보면, 행렬에서 아래와 같은 위치를 가진다.

빗금친 행렬의 요소를 추출하기 위해서 for문을 돌리기보다는, Huang이 소개한 Skewing을 통해서 추출할수 있다.

자세한 방법은 다음과 같다.

실제로 그림을 그려서 어떻게 가능한지에 대해서 확인해보면, 아래와 같다.

이렇게 Skewing을 통해서 RPR을 구하는데 더욱 효과적으로 메모리를 관리 할 수 있다.
Skewing을 사용하여 RPR과 MHA를 구현해보면 이를 이해하는데 더욱 도움이 될 것 같다.
다음 글은 Llama2에 적용된 Rotary Embedding에 대해서 설명해보고자 한다.
-
Airflow task를 ECS Fargate task로 실행하기(Airflow ECSOperator)
Airflow의 확장 Provider인 apache-airflow-providers-amazon의 ECSOperator를 사용하여 Airflow DAG내 Task들을 컨테이너로써 실행시킬 수 있다. Airflow KubernetesExecutor를 사용할때와 동일하게 이미지로 task 컨테이너를 띄워 Pod로 돌리듯이 ECS에 Airflow 테스크를 정의하여 실행시키면 된다. 이러한 방법으로 얻는 이점은 1. 테스크를 Fargate로 실행시키므로써 task를 실행시킬 컨테이너를 띄울 노드 인스턴스를 항시 켜놓지 않아도 작업이 필요한 순간에만 컴퓨팅을 하기 때문에 비용을 절감할 수 있다. 2. Fargate 테스크가 Airflow task마다 각각 실행되어 독립된 환경에서의 task실행을 보장할 수 있다. 또한 각각의 task마다 필요한만큼 따로 용량 프로비저닝도 가능하여 유연한 작업 실행 환경을 구성할 수도 있다. 우선 테스크 컨테이너를 실행할 ECS 클러스터를 생성한다. 클러스터에는 기본적으로 Fargate, Fargate SPOT 용량공급자가 사용 가능하다. 필요시 EC2 인스턴스, 또는 외부 인스턴스 용량 공급자도 같이 선택할 수 있다. ECS에서 말하는 용량 공급자란 필요한 서비스 또는 테스크 컨테이너를 띄워줄 수 있는 인프라를 말한다. 클러스터를 생성했다면 Airflow를 구성한다. Airflow를 실행하는 방법은 여러가지가 있으나 해당 글에서는 다루지 않음 Airflow에 AWS 커넥션을 구성해야 한다. 이 또한 여러 방법이 있지만 Airflow conn을 구성하지 않고 기본 커넥션으로 airflow.cfg에 구성하는 방법을 사용함 - AIRFLOW_CONN_AWS_DEFAULT={"conn_type":"aws","login":"<AWS 액세스키>","password":"<AWS 비밀키>"} - AWS_DEFAULT_REGION=<AWS 기본 리전> 위와같이 환경변수를 구성하여 컨테이너에서 Airflow를 실행하는 방법 아래는 DAGRun API를 통해 비동기로 실행되는 DAG 예제 코드이다. import sys sys.path.append("/opt/airflow") import pendulum from airflow import DAG from airflow.operators.empty import EmptyOperator from airflow.utils.trigger_rule import TriggerRule from airflow.providers.amazon.aws.operators.ecs import ( EcsRegisterTaskDefinitionOperator, EcsRunTaskOperator, ) from src.config import SUBNET_MAPPED_2A_PRIVATE, SUBNET_MAPPED_2B_PRIVATE # Constants DAG_ID = "ECS-FARGATE-DAG" AWS_REGION = "ap-northeast-2" ECS_CLUSTER = "test" DOCKER_IMAGE = "<Conatiner Image URL>" AWS_LOG_GROUP = "/ecs/test" default_args = { 'owner': 'airflow', 'depends_on_past': False, 'start_date': pendulum.now(), 'retries': 0, } task_definition_params = { "requiresCompatibilities": ["FARGATE"], "cpu": "4096", "memory": "30720", "runtimePlatform": {"operatingSystemFamily": "LINUX", "cpuArchitecture": "X86_64"}, "networkMode": "awsvpc", "executionRoleArn": "<AWSRoleARN>", } network_configuration = { "awsvpcConfiguration": { "subnets": [<사용할 subnets>], } } def create_ecs_operator(task_id, cpu, memory, trigger_rule=TriggerRule.ALL_SUCCESS): return EcsRunTaskOperator( task_id=task_id, cluster=ECS_CLUSTER, task_definition=task_definition.output, launch_type="FARGATE", network_configuration=network_configuration, overrides={ "containerOverrides": [ { "name": "test", "environment": [ {"name": "param", "value": "{{ dag_run.conf['param1'] }}"}, ], "command": ["python", "main.py", "--task", task_id], "cpu": cpu, "memory": memory, } ] }, trigger_rule=trigger_rule, ) with DAG(DAG_ID, schedule=None, max_active_runs=100, default_args=default_args) as dag: task_definition = EcsRegisterTaskDefinitionOperator( task_id="task_definition", family="test", container_definitions=[ { "name": "test", "image": DOCKER_IMAGE, "logConfiguration": { "logDriver": "awslogs", "options": { "awslogs-region": AWS_REGION, "awslogs-group": AWS_LOG_GROUP, "awslogs-stream-prefix": "REPORT", "awslogs-create-group": "true", }, }, }, ], **task_definition_params ) task1 = create_ecs_operator("task1", 256, 512) task2 = create_ecs_operator("task2", 256, 512) # Define dependencies task1 >> task2 - 정의된 task_definition에 각각의 테스크에 추가로 containerOverrides를 정의하여 필요한 용량 프로비저닝 등을 설정한다.
-
[AWS] - Large Dependencies with AWS Lambda
간단한 서비스를 배포하기 위해 AWS를 사용하던 도중, Fast API와 같은 서비스가 아닌 최소한의 로직만을 품은 서비스를 배포해야하는 상황이 자주 발생하였다. 개발 싸이클의 최소화를 위해 AWS Lambda를 사용하여 서비스를 배포하며 겪은 시행착오와 해결 방법을 회고하고자 한다. 데이터 분석을 위한 이 서비스는 로우데이터를 가공하고 변형하여 Graph 형태 (https://en.wikipedia.org/wiki/Graph_theory)로 변환하고, GPT를 활용한 보조를 포함한 서비스이다. 이를 위한 requirements는 아래와 같다 위의 패키지들을 로컬과 개발 서버에서 사용하는데에는 문제가 없지만 AWS Lambda에서는 중요한 문제가 발생했다. 해당 문제는 다음과 같다
-
How to get a GCP service account key - 구글 서비스 계정 key json 발급받기
GCP(Google Cloud Platform) 서비스 계정 키 JSON을 발급받는 방법을 다섯 가지 단계로 설명해드리겠습니다. 1. Google Cloud Console에 로그인 먼저 Google Cloud Console에 로그인합니다. 계정에 액세스하려면 유효한 Google 계정이 있어야 합니다. 2. 서비스 계정 생성 왼쪽 상단의 네비게이션 메뉴에서 "IAM 및 관리" 섹션으로 이동한 후 "서비스 계정"을 선택합니다. "서비스 계정 만들기"를 클릭하여 새 서비스 계정을 생성합니다. 3. 권한 부여 서비스 계정에 적절한 역할(권한)을 할당합니다. 필요에 따라 프로젝트나 리소스에 대한 권한을 설정할 수 있습니다. 4. 키 생성 생성된 서비스 계정을 선택하고 "키 추가"를 클릭합니다. JSON 형식의 키 파일을 선택하고 키를 만듭니다. 5. JSON 다운로드 키가 성공적으로 생성되면 JSON 파일이 다운로드됩니다. 이 파일은 GCP API와 통신할 때 사용되며 안전하게 보관해야 합니다. 이렇게 하면 GCP 서비스 계정 키 JSON을 성공적으로 발급받을 수 있습니다.
-
helm chart로 Airflow 운영 시 log를 AWS S3에 저장하기
안녕하세요. Airflow 를 helm chart를 이용하여 운영하고 있는데요. 이번에는 Airflow를 운영하면서 쌓이는 log 들을 DB가 아닌 AWS S3에 저장하는 방법을 소개시켜드리려고 해요. 이 글을 읽으시는 분들은 이미 Airflow를 운영하면서 사용하시는 helm chart, 즉 yaml 파일 하나를 가지고 있으실 텐데요. AWS S3에 연결하기 위해서는 yaml 파일에서 설정을 살짝 바꿔야합니다. 위 사진 처럼 remote_logging 부분에 'True', remote_base_log_folder 부분에 사용하실 S3 주소를 넣으면 된답니다. 그리고 remote_log_conn_id 에는 사용하실 id값을 자유롭게 적으셔도 돼요. 이렇게 수정을 하고 다시 helm chart를 업데이트 해줍니다. 이제 남은 것들은 굉장히 간단합니다. Airflow web으로 접속 한 뒤 [Admin > Connections] 메뉴를 클릭합니다. 새로운 항목을 추가할건데 위 사진처럼 Connection_id에 yaml파일에 설정한 remote_log_conn_id를, Connection Type은 Amazon Web Services를 선택해주고, AccessKey와 Secret Access Key는 사용하는 값들을 잘 입력해주면 됩니다. 이렇게하면 Airflow에서 나오는 log들이 S3에 저장됩니다.
-
[Nginx, FastAPI, gunicorn] gunicorn timeout 트러블슈팅
AWS ElasticBeanstalk로 배포한 FastAPI 앱에서 1분 이상 걸리는 작업을 배포된 AWS Lambda를 통해 진행시키는데, 어느날 해당 API 호출이 실패하며 ElasticBeanstalk에는 아래와 같은 로그가 남아있었다. 2024/03/22 02:57:45 [error] 1112907#1112907: *88 upstream prematurely closed connection while reading response header from upstream, client: x.x.x.x, server: , request: "POST /cross-selling HTTP/1.1", upstream: "http://127.0.0.1:8000/cross-selling", host: "keywordsearch.pluszero.co.kr", referrer: "https://keywordsearch.pluszero.co.kr/crossselling" FastAPI 앱을 운영 서버에 배포하면 일반적으로 아래와 같은 구성으로 배포한다 즉 nginx에서 error.log에 남긴 로그는 업스트림 서버(WSGI HTTP Server 또는 Python Application)에서 준 응답 헤더를 읽는 도중 커넥션이 닫혀버렸다는 것이다. 위 현상은 응답까지 오래걸리는 lambda를 사용한 API에서만 발생하기 때문에 timeout 이슈라고 판단했다. 그래서 다시 ElasticBeanstalk의 web.stdout.log를 확인해 보니 아래와 같은 로그가 남아있었다. Mar 22 02:57:44 ip-10-0-3-4 web[1112864]: [2024-03-22 02:57:44 +0000] [1112864] [CRITICAL] WORKER TIMEOUT (pid:1112896) Mar 22 02:57:45 ip-10-0-3-4 web[1112864]: [2024-03-22 02:57:45 +0000] [1112864] [WARNING] Worker with pid 1112896 was terminated due to signal 9 해당 요청을 처리하는 gunicorn의 worker가 timeout으로 인해 강제로 종료된 것이다. gunicorn worker의 timeout 설정을 바로하여 문제를 해결할 수 있었다. 아래는 수정된 ElasticBeanstalk에서 서버를 시작하는 Procfile 내 명령어이다. web: gunicorn --bind 0.0.0.0:8000 -k uvicorn.workers.UvicornWorker main:app --timeout=180 api별로 응답 timeout 시간을 설정할 수 있다면 좋겠지만, FastAPI가 아닌 WSGI gunicorn 서버에서 발생하는 오류이므로 전역으로 설정할 수 밖에 없는 문제였다.
-
Adobe Analytics API로 데이터 추출하기(2)
안녕하세요 지난 글에 이어서 Adobe Analytics API로 데이터를 추출해볼건데요. 지난 글에서는 가이드에 있는 그대로 기본 지표들을 뽑아봤는데, 이번에는 내가 만든 커스텀 값, 계산된 지표들을 뽑아보려고해요. 먼저 가이드는 아래 가이드를 참고했습니다. https://developer.adobe.com/analytics-apis/docs/1.4/guides/reporting/report-description/dimensions/ https://developer.adobe.com/analytics-apis/docs/1.4/guides/reporting/report-description/metrics/ evar값을 찾아서 넣어볼건데요. 저 같은 경우는 evar5 에다가 CID를 수집을 하고있어요. 그래서 그 값을 추출해보려고 합니다. 최종적으로는 CID별 방문 수에 대해서 알아보려고 해요 지난 글에서는 dateRange였지만 위 사진처럼 내가 추출하고자 하는 변수 명을 넣어줍니다. 저는 evar5를 추출하고싶기 때문에 evar5를 써줬어요. 예시를 dimension에 대해 작성하였지만, metric도 방법이 같아요. 가이드에서 사용하고자 하는 값을 찾고 그 명칭으로 넣으시면 돼요 이상으로 Adobe Analytics API를 사용해서 원하는 디멘션, 메트릭 값 추출하는 방법 마치겠습니다.
-
Python pandas 모듈의 DataFrame 객체를 Google Bigquery로 로드하기
구글에서 제공하는 google-cloud-bigquery SDK를 사용하거나, 임의의 데이터를 가진 DataFrame 인스턴스 df가 있다고 가정할 때, 데이터프레임 인스턴스에서 바로 to_gbq 메소드를 호출하여 빅쿼리로 데이터프레임의 내용을 로드할 수 있다. dtype BigQuery Data Type i (integer) INTEGER b (boolean) BOOLEAN f (float) FLOAT O (object) STRING S (zero-terminated bytes) STRING U (Unicode string) STRING M (datetime) TIMESTAMP credentials, destination_table 등의 기본적인 정보만 세팅하면 간단하게 빅쿼리로 데이터를 로드할 수 있으나, 내부적으로는 데이터프레임으로부터 로컬에 임시 csv 파일을 생성하고, 이를 빅쿼리에 로드하는 방식으로 영문 컬럼명이 아닐 경우 인코딩 문제, 데이터프레임에서 NaN 결측치가 포함된 컬럼의 경우 NaN은 부동소수 데이터타입으로 컬럼 데이터타입이 integer가 될 수 없는 문제 등 몇가지 단점이 존재함 SDK를 통해 직접 데이터를 로드하는 방식 워크플로우는 다음과 같음 - credentials의 project에 데이터셋, 테이블 존재여부 확인 및 생성 - 스키마가 정의된 테이블로 데이터 로드 마지막 단계에서 데이터를 로드할 경우 사용할 수 있는 방식은 다음과 같음 - client.insert_rows_from_dataframe 메소드 사용 insert_rows_from_dataframe 메소드의 경우 pandas-gbq 모듈에서 발생한 문제가 동일하게 생길 수 있으므로 특히 pd.Timestamp 시계열 데이터, NaN(numpy) 등이 객체타입이므로 해당 데이터들은 문자열 등의 타입으로 변환하고 dict 객체로 캐스팅해야함(NaN의 경우 None으로 대체) insert_rows_from_*은 대량의 데이터를 업로드할 시 오류가발생함
-
Adobe Analytics API로 데이터 추출하기(1)
어도비에서 작성한 문서가 있어 이 문서를 참조하여서 진행했습니다. https://developer.adobe.com/analytics-apis/docs/2.0/guides/ 먼저, Developer Console에서 API Client를 생성해야합니다 개발자 콘솔에서 [Create new project] 를 클릭합니다. [Add API] 를 클릭하고 [Adobe Analytics]를 클릭합니다. 그리고 생성한 프로젝트에 들어가서 "client_id", "client_secret", "scope" 를 잘 복사해둡니다. Adobe Analytics API에 접근하려면 어도비가 접근을 허용해준 토큰을 가지고 있어야 하는데요. 토큰을 발급받는 방법을 소개 드리겠습니다. https://developer.adobe.com/developer-console/docs/guides/authentication/ServerToServerAuthentication/IMS/ 위 링크에 들어가면 해당 사진 처럼 나옵니다. 가이드에는 curl 명령어로 나와있지만 나는 해당 명령어를 파이썬으로 작성하여 사용하였습니다. 함수로 작성을 하였는데, 인자로 아까 복사해둔 client_id, client_secret, scope 을 전달하면 됩니다. 이제 access token을 발급 받았다면 adobe analytics 데이터를 추출할 준비가 끝났습니다. https://developer.adobe.com/analytics-apis/docs/2.0/apis/ 위 가이드를 보고 사용하고 싶은 api를 선택하여서 사용하면 됩니다. 저는 Reports api를 사용하여 데이터를 추출해보려고 합니다. 가이드에 있는 curl 명령어를 보고 파이썬으로 추출해보겠습니다. 이렇게 작성하시고 데이터를 추출하시면 됩니다. 이상으로 Adobe Analytics Api를 활용하여 기본적인 데이터 추출을 작성하였습니다. 다음 글에서는 필터, 디멘션, 메트릭 같은 지표를 설정하는 법에 대해 알아보겠습니다.
-
[ML/DL] Transformer - Rotary Encoding
이번글은 이전 Relative Positional Embedding의 단점을 보완하고, 최근 LLM모델에서 많이 사용되는 Rotary Positional Encoding (RoPE) 에 대해서 리뷰해보려 합니다. 이전에 소개했던 Absolute Positional Encoding, Relative Postional Embedding과 Encoding과 Embedding의 차이를 다시 짚어보면, Encoding은 모델 학습중에 변하지 않는 값이며, Embedding은 모델이 학습을 통해 변하는 파라미터이다. Absolute Positional Encoding은 sinusodial 함수를 통해 토큰의 순서에 대한 정보를 전달한다. 그러나 이러한 방식은 토큰간의 거리에 대한 정보를 포함하고 있지 않기에 기준이 되는 토큰에서 가까운 토큰과 먼 토큰에 대해서 동일하게 본다. Relative Positional Embedding은 Absolute Positional Encoding에서의 단점인 토큰간의 거리에 대한 정보를 추가하고 학습시에 순서에 대한 정보가 변경되는 Embedding 방법을 사용하였다. 그러나, 이러한 방식은 모델의 학습시 계산량이 늘어나며 비효율적 (Computationally Inefficient)하고, 모델을 사용하여 추론을 할 때에 Positional Embedding이 계속 바뀌어서 추론시에 적합하지 않다는 의견이 있다. 이번에 소개할 Rotary Positional Encoding은 위의 두가지 방법의 단점을 보완한 방법으로 RoFormer라는 모델에서 처음 소개되어 현재는 Llama2, PaLM등에서 많이 사용된다. Roformer: Enhanced Transformer with Rotary Position Embedding - https://arxiv.org/abs/2104.09864 Rotary Encoding은 삼각함수에서의 Rotation Matix를 이용한다. 위의 예시에서, [x,y]에 해당하는 벡터가 θ (세타)값에 따라 원을 따라 로테이션 하는 것을 볼 수 있다 아래 그림은 Radius가 1인 원에서의 cos(thetha)와 sin(thetha)를 시각화 한 것이다. Rotation Matrix에 대해서 이해 했다면, 간단한 예시를 들어 Rotary Encoding을 이해해보자. Token이 임베딩 레이어를 들어가서 나온 결과가 [b, seq, 2]로, 각 토큰이 2개의 벡터값으로 임베딩이 됬다는 가정으로 확인해보자. Vaswani의 트랜스포머 모델의 Q, K, V는 행렬인데, 이를 백터화 하여 표현하자면 아래와 같다. q의 m번째 순서는 f_q를 통해 나타나는 값, 이며 k, v도 동일한 의미이다. 따라서, q_m은 [1, 2]의 값을 가진다. 만약 문장의 길이가 5라면, Q는 [5, 2]의 크기를 가진 텐서가 된다. 벡터와 매트릭스의 표현을 주의하여 보면, RoFormer에 적용된 f_q는 아래와 같다. 위의 수식에서 m은 해당 토큰의 순서이다. 예를 들어, [ i, like, the, transformer] 라는 4개의 토큰이 있다면, i = 1, like = 2, the = 3, transformer = 4 라는 m값을 가진다. thetha는 아래와 같이 정해진 값을 따른다. 여기서 i는 d/2이며, d 는 벡터의 dimension이다. 간단한 예제에서는 각 토큰이 2-d로 표현 되었기에 d=2가 되고, i = 1 하나의 값만 가진다. 따라서 Θ = {1}값 하나이다. 이에 따라 각 m에 해당하는 토큰들의 값을 로테이션을 해준다고 보면 된다. 여기에서 생기는 의문점은, 위와 같이 Position에 대한 값이 Encoding이 되었는데, 어떻게 Relative Position에 대한 정보를 주느냐? 라는 의문이 생길수 있다. 이는 아래 그림을 통해 알아 볼 수 있다. https://www.youtube.com/watch?v=o29P0Kpobz0 위의 그림과 같이, 3개의 문장이 있다. [dog] [the dog] [the pig chased the dog] 이 문장에서 우리는 dog라는 단어에 포커스를 맞추면, 단어가 출현하는 순서에 따라 fig.1의 dog의 백터값이 변화한다. 여기서 가장 중요한것은 fig.4인데, pig와 dog의 거리는 2를 보여준다. [the pig chased the dog] [once upon a time, the pig chased the dog] 그러나, 각 pig와 dog가 문장에서 출현하는 위치는 다르다 1번문장의 pig는 m=2, dog = 5 2번 문장의 pig는 m=6, dog=9 각 문장에서 해당 단어가 가지는 로테이션은 다르지만, 동일한 거리의 차이로 인해 두 단어의 각도의 차이는 동일하다. 이 부분이 단어간의 거리에 대한 정보를 포함한다고 보는 점이다. 다시 수식을 보면, f_q를 구할때 단순 Thetha가 아닌 포지션인 m을 곱한 값을 통해 rotation matrix를 만든다 [cos(mθ) -sin(mθ) ] [ sin(mθ) cos(mθ)] 어떠한 방식으로 Rotary Encoding이 생성되는지 이해 했다면, 이번에는 2-D 이상의 값으로 생각해보자. 여기서 발생하는 문제는, 3차원으로보게 된다면, Rotation matrix는 더이상 단순하지가 않다.. 3차원만 해도 수식이 복잡해지는데, 4차원, 등등 더욱 고차원으로 올라갈수록 input을 로테이션하기 위한 매트릭스는 더 복잡해진다. 더욱이, 대부분의 LLM에서 사용하는 차원수는, 1024가 넘어간다. Llama의 경우 4096의 d 를 가졌다. 다행인점은 대부분의 모델들의 차원이 짝수개를 이룬다는 것이다. (even number) 대부분은 2의 제곱 형태로 증가한다. 이러한 문제를 해결하기 위해서, Roformer에서 고안한 방법은 고차원의 벡터를 2개씩 decompose하여 2개의 백터에 대해서 로테이션을 진행하는 방법이다. 위와 같이 정형화된 형식으로 Rotary Encoding 을 만들면 이렇게 만들수 있다. 인풋으로 들어오는 문장에서 단어의 최대 길이만큼 (context_window)의 R이라는 Rotary 텐서를 생성후에 Q, K, V 값을 연산한다. 이를 적용한 Attention Block은 아래와 같이 쓸수 있다. 자세한 코드는 아래주소에서 찾아볼수 있다 https://github.com/bkitano/llama-from-scratch/blob/main/llama.ipynb 이러한 방식으로 Rotary Encoding을 구현 할 수 있으나, Roformer에서 이런 R을 만드는 general form은 연산시 효율이 좋지 않아 다른 방법을 제안해 주었다. 연산의 효율을 올리기 위해서는 Roformer의 식을 다시 볼 필요가 있다. Roformer에서 사용하는 방법은 복소수 (Complex Number)를 사용하여, 오일러 공식을 사용하는 방법이다. 위에서 들었던 간단한 예제를 보면, 2-D의 벡터는 Complex Number로 볼수 있다. 예를 들면, [1, 2]라는 Real Number를 Complex Number로 보게 되면, 1+2i (i = imaginary number)로 표현된다. 오일러 공식은 아래와 같다 특히 오일러 공식은 Rotation과 벡터의 변환 및 연산을 간략화 할 수 있다. 따라서 complex number를 사용하여 벡터의 로테이션을 진행해보면 다음과 같은 시각화 결과를 얻을수 있다. 위의 시각화는 아래의 코드를 통해 얻을수 있다. Complex Number를 사용함으로써 행렬곱이 아닌 [ (a + bi) * (sin(thetha) + cos(thetha)i ] 처럼 간략화 될수 있다. Dimension관련해서 연산하는 방법이 이해가 됬다면, 이번에는 sequence length = 3인 문장에 대해서 로테이션을 진행해보자. 중요한점은 이러한 Complex Number를 생성할때 Cartesian coordinates와 상응하는 polar coordinates를 생성해주는것이 중요하다. pytorch 에서는 polar라는 메소드를 사용 할 수 있다. 위의 매소드를 사용할때에는 abs값을 1. 로 사용한다. 이러한 점을 사용하면, wq를 구하는 것을 간략화 할수 있다. 이러한 방법으로 Rotary Encoding을 구현할수 있으며, 정확한 코드는 Llama 코드에서 확인해볼수 있다. https://github.com/facebookresearch/llama/blob/main/llama/model.py
-
[ML/DL] Transformer - Relative Positional Embedding
이번 글은 이전 Vaswani의 트렌스포머에서 사용되었던 Absolute Positional Encoding의 단점을 보완하기 위해 연구된 Relative Positional Embedding에 대해 리뷰해보려 한다. Vaswani의 트렌스포머 아키텍처와 비슷하지만 이번 Shaw et al의 Self-Attention with Relative Position Representations(https://arxiv.org/abs/1803.02155)는 기존의 아키텍처에서 조금의 변경사항이 있다. 가장 큰 변경사항은 Positional Encoding대신에 사용된 Relative Positional Embedding의 사용과 함께 기존의 Self-Attention 메카니즘의 연산에서의 추가 사항이 있다. 이번글에서는 Vaswani의 아키텍처에서의 Self-Attention 연산과의 차이점과 Relative Positional Embedding에 대해서 설명해보려 한다. 우선 기존 트렌스포머는 Token Embedding과 Positional Encoding의 합을 Self-Attention에 적용한다. 위의 수식에서 z는 self-attention의 결과이며, 아래 수식은 Scaled Dot-Product Attention을 통한 Attention Score를 구하는 방법이다. 자세한 설명은 Vaswani의 Attention is all you Need에서 찾아볼수 있다. 다음은 Relative Positional Representation에서의 Positional Embedding을 함께 사용하여 연산하는 Self Attention이다. e_ij와 z_i를 구할때 2개의 Relative Positional Embedding을 추가하여 Self Attention을 적용하였다. 위의 수식에서 e_ij를 구할때 추가된 (a_ij^k)와 z_i를 구할때 추가된 (a_ij^v) 2개의 요소가 Positional Embedding이다. e_ij를 구한이후 Vaswani의 수식에서 a_ij를 구하는것은 동일하다. 그렇다면, 이 논문에서 얘기하는 Relative Position이란 무엇인가? 예를 들어서 5단어로 이루어진 어떠한 문장이 있다고 가정하고, 이를 토큰화를 진행하였다. 그랬을때 우리는, [A, B, C, D, E]라는 순서를 가진 Input을 가졌다고 가정하였을때, 각 단어들의 거리 (Distance)를 통하여 Relative Postional Representation (RPR)을 구한다고 한다. 위의 예시에서 A는 B, C, D, E 의 거리 B는 A, C, D, E 의 거리를 구하며, 자기 자신의 거리또한 구한다. 여기서 중요한점은 C를 기준으로 A,B,D,E와의 거리를 구할때 A,B는 C의 앞에, D와 E는 C의 뒤에 나왔는데, 이러한 순서도 중요하게 보아야 한다. 따라서 5개의 단어에 대해서 나타낼수 있는 거리는 앞으로 4단어, 뒤로 4단어, 자기 자신인 총 9개의 거리를 구할수 있다. 총 9개의 거리에서 0은 기준이 되는 단어에서 4단어 앞에, 1은 3단어 앞에 2는 2단어 앞에 3은 1단어 앞에 4는 자기 자신으로, 5는 1단어 뒤에 6은 2단어 뒤에 7은 3단어 뒤에 8은 4단어 뒤에 이런 경우의 수가 나타난다. 오른쪽은 0부터 8까지의 인덱스에 대한 설명이며, 왼쪽에 있는 행렬이 "Distance Matirx"라고 한다. 논문에서는 최대 몇 단어까지 RPR을 볼것인지 규정하는 K라는 변수가 있다. 보편적인 NLP의 학습시에는 문장의 길이가 위의 예시랑은 다르게 꽤 길기 때문에 이에 대한 고찰이 있었는데, 논문상에서는 꽤나 큰 차이를 보여주지 않은것 같다. 구현을 하며 Shaw et al 의 RPR에 대해 심층적으로 이해해 보자면, 우선 가상의 데이터와 파라미터를 설정해보자. 간단한 구현을 위해서, Batch Size = 2 Sequence Length = 5 Embedding Dimension = 12 논문의 k = 5 따라서 Input의 크기는 [b, s, d] 인 [2, 5, 12]의 크기를 가지는 텐서이다. [1] 학습에 따라 값이 변하는 Parameter를 초기화 해준다. 해당 파라미터는 학습에 진행되는 {2*최대 단어길이 + 1}이며, 5개의 단어를 정해놓았다면, 11개로, 이는 논문에서 얘기하는 2k+1을 따랐다. 초기화된 파라미터는 (2s+1, d)의 크기를 가진다 [11, 12] [2] Distance Matrix를 생성한다. 행벡터와 열벡터의 연산으로 Distance Matrix를 구할수 있다. 이후 논문 3.2에서 얘기한 clip(x, k)를 진행한다. 만약 K가 4보다 작다면, 4보다 큰 값은 최대 값으로 고정된다. 예를 들면 k를 3으로 하였을때 -4, 4는 사라지고, 3과 -3으로 변경되었다 [3] Clamp된 Distance Matrix를 구했다면, 해당 값을 음수가 아닌 양수로 바꿔준다. 따라서 Distance Matrix에 K를 더해준다. 아래 예제에서는 k=5를 사용한것을 기본으로 한다 [4] Distance Matrix는 거리에 따른 임베딩값의 Index에 대한 값을 가진 행렬임으로, [1]에서 초기화 하였던 Embedding Table에서 Distance Matrix의 인덱스에 해당하는 임베딩을 가져온다. [5] Positional Embedding을 추출했다면, 논문에서 제안한 e_ij에 대한 연산을 진행해보자. xW{Q}는 [b, s, d]의 크기를 가진 텐서이고, xW{K}도 [b, s, d]의 크기를 가졌다. 두 텐서의 Dot Product를 위해 xW{K}의 Transpose를 진행하면 [b, s, s]의 크기를 가진 텐서가 나온다. xW{Q}와 Embedding의 연산은 바로 되지 않기에 xW{Q}[b, s, d]와 Embedding [s, s, d]를 조금 변경해준다. xW{Q}는 [b, s, 1, d]로 변경해주고, Embedding은 Transpose를 취해준다 [s, d, s] 두 텐서의 Dot Product는 [b, s, 1, s]로 나타나고, 추가했던 2번째 디멘션을 제거한다. 예시를 위해 wq와 emb는 random값으로 초기화 하여 연산의 가능성만 확인하였다. 아래 구현에서는 MultiHead를 포함한 구현 예시이다. 다른 구현은 여기에서 볼수 있다. https://github.com/evelinehong/Transformer_Relative_Position_PyTorch/blob/master/relative_position.py 이렇게 해서 Relative Postional Embedding을 통한 Multi Head Attention을 사용할수 있다. 그러나, 2018 12월에 Huang의 논문에서 이러한 방식의 구현이 GPU 메모리에 과도한 점유율을 보여주는점을 시작으로, RPR을 개선하는 논문을 발표했다. Shaw의 논문은 2018 4월에 발표되었고, Huang의 논문은 2018 12월에 발표 되었다. Music Transformer (https://arxiv.org/abs/1809.04281) Huang은 Skewing Mechanism으로 GPU 메모리를 더 효율적으로 사용하는 Relative Positional Attention을 소개하였다. 가장 중요한 핵심은, Distance Matrix에서 임베딩을 가져오는 부분이다. 우선 위에서 했듯이 우리는 (2s+1, d)의 임베딩 테이블을 초기화 했으나, 정작 사용하는 임베딩은 (2s-1)개 이다. 5개의 단어로 예를 들면 앞으로 4개, 뒤로 4개, 자신 1개 (총 9개)를 사용한다. 따라서 임베딩 테이블을 (2s-1, d)로 초기화를 해준다. 그 다음, scaled dot product연산을 진행한다. q_emb는 [b, s, 2s-1]의 값을 가지고 있다. 예시의 값은 [2, 5, 9]이며, 모든 RPR을 생각해보면, 아래 그림을 그려볼수 있다. 왼쪽의 테이블처럼, 첫번째 단어는 [4,5,6,7,8]의 인덱스, 두번째 단어는 [3,4,5,6,7]의 인덱스를 가진다. 조금더 크게 확장해보면, 행렬에서 아래와 같은 위치를 가진다. 빗금친 행렬의 요소를 추출하기 위해서 for문을 돌리기보다는, Huang이 소개한 Skewing을 통해서 추출할수 있다. 자세한 방법은 다음과 같다. 실제로 그림을 그려서 어떻게 가능한지에 대해서 확인해보면, 아래와 같다. 이렇게 Skewing을 통해서 RPR을 구하는데 더욱 효과적으로 메모리를 관리 할 수 있다. Skewing을 사용하여 RPR과 MHA를 구현해보면 이를 이해하는데 더욱 도움이 될 것 같다. 다음 글은 Llama2에 적용된 Rotary Embedding에 대해서 설명해보고자 한다.
-
[ML/DL] Transformer - Positional Embedding
최근 인공지능 분야에서 가장 큰 트렌드는 LLM (Large Language Model)로, 우리가 많이 사용하는 Chat GPT, Bard등 다양한 분야에서 활용하는 언어모델이다. 대부분의 LLM의 기원은 Vaswani의 Transformer 아키텍처(2017) (https://arxiv.org/abs/1706.03762) 를 기본으로하며, 해당 연구는 NLP에서 사용되던 RNN계열인 GRU 또는 LSTM보다 우수한 성능을 보여주며 많은 분야에 적용되고 있다. 대부분의 LLM이 Vaswani의 Transformer를 사용하지만, 지속되는 연구를 통해서 조금씩의 차이를 보여주고 있다. 대표적으로는 기본 Transformer 아키텍처에서는 Multi-Head Attention이후의 값을 Normalization을 하는 "Post Normalization" 방식과 Meta에서 공개한 Llama2에서는 Multi-Head Attention 이전에 "RMS norm"을 적용하여 "Pre Normalization"을 사용하는 방법이 있고, Activation 함수는 ReLU를 사용하던 기존에서, "SwiGLU"를 사용 하는 방법 등 다양한 차이점이 있다. 이 글은 이러한 차이점 중에서 Positional Encoding / Embedding (PE) 에 대해서 집중적으로 설명을 해보려고 한다. 이번글은 1. 왜 PE가 필요한지 2. Encoding과 Embedding의 차이점 3. Vaswani의 PE에 대한 이해 4. Vaswani의 PE의 장점과 단점 추후에는 이 PE의 단점을 보완한 Relative PE와 Llama에 적용된 Rotary PE에 대한 글을 작성할 예정이다. 위의 Figure 1은 Vaswani의 Transformer 아키텍처로, inputs은 Token의 Sequence이며, 해당 토큰은 Embedding Table을 통해 Token Embedding을 생성한다. 이후 Pre-Define된 Positional Encoding과 합연산을 통해 각 토큰의 순서에 대한 정보를 값에 포함시키는 것이다. [1] 그렇다면, 왜 Transformer는 PE가 필요했을까? 이에 대해서는 RNN계열의 단점을 봐야한다. 위의 그림은 기본적인 RNN 계열의 연산 방법이다. 간략하게 설명하자면, x<1>이 들어가서 a<0>과 함께 연산이 되어(파란색 블럭) 이에 대한 결과는 y<1>과 오른쪽의 파란색 블럭의 인풋 a<1>로 사용된다. x<2>는 x<1>이 연산된 결과와 함께 연산되어 y<2>, a<2>로 나타난다. 이러한 방식을 모든 x 까지 하게 되어 나온 y은 앞에 연산된 a<1>부터 들어간 값이 함께 연산이 되었기에 x들에 대한 정보를 가지고 있다고 생각할수 있다. 그러나 RNN계열의 연산 방식은 모든 x의 순서 (Sequence)를 거치면서 연산속도에 대한 단점과, Input의 Sequence가 길다면 앞의 정보를 잃어버리는 경우가 발생한다. 이를 보완하기 위해 GRU, LSTM등 다양한 RNN계열의 네트워크가 있지만 비슷한 문제점이 발견되어 왔다. 간단하게 생각하면 이러한 문제점을 보완하기 위해 연구된 결과가 Transformer 아키텍처이다. 문제는 이 Transformer의 내부 구조는 Sequence에 대한 정보를 전달하는 연산과정이 없다. 모든 레이어의 컴포넌트는 Fully Connected 구조로 Input에 대한 수치와 layer가 가지고 있는 가중치(W)의 행렬곱으로 연산이 되는 구조이기에 Sequence에 대한 정보를 주입해 주는 과정이 필요했다. 예를 들자면, "트렌스포머는 최고의 아키텍처이다"와 "마이클 베이의 트렌스포머는 최고다" 에서 순서를 상관하지 않는다면, "트렌스포머"라는 단어는 동일한 임베딩 값을 가질것이다. 임베딩 값은 모델의 학습이 진행되며 값이 변하지만, 고유한 인덱스는 변하지 않는 테이블이라 생각하면 쉽다. 위의 예시는 10개의 단어에 대한 5개의 임베딩 값이다 만약 위의 두 문장을 넣는다면, "트렌스포머"라는 단어가 3번 인덱스에 해당한다면, [0.9, 1.37, -0.16, -0.2, 0.7]이라는 벡터가 "트렌스포머"라는 단어의 값이다. (인덱스의 시작은 0부터) 다른 예시를 들자면, "트렌스포머 아키텍처와 트렌스포머 영화는 다르다" 라는 문장에서 "트렌스포머"라는 단어는 다른 의미를 가진 단어가 되어야 한다. 이를 위한 방법이 Positional Embedding이다. 그런데, Vaswani의 아키텍처에는 "Positional Encoding"이라고 명시되어 있는 부분이 있다. [2] "Positional Encoding"과 "Positional Embedding"은 무슨 차이가 있을까? Encoding과 Embedding은 모델의 학습과정에서 값이 변하는지에 대한 유무에 따라 달라진다. Encoding이란 학습이 진행됨에 따라 변하지 않는 값이고, Embedding은 모델의 학습에 따라 Gradient Descent (경사하강법)을 통해 값이 변하는 Parameter이다. [3] Vaswani의 트렌스포머 아키텍처에서 Positional Encoding이라 명시한 이유는, Input의 길이에 대한 각 포지션(순서)에 대해서 값을 지정한다. pos는 문장에서 단어의 위치이며, i는 임베딩 디멘션이다. Input에 대한 예시를 들어보면 "트렌스포머는 vaswani가 연구한 아키텍처이다"를 단어별로 토큰화 하게 되면, "트렌스포머는 vaswani가 연구한 아키텍처이다" -> [트렌스포머는, vaswani가, 연구한, 아키텍처이다]로 4개의 문단어를 가진다. 각 단어에 고유한 번호를 부여하면, [트렌스포머는, vaswani가, 연구한, 아키텍처이다] -> [0, 1, 2, 3]으로 간단하게 볼수 있다. 이러한 변환을 토큰화 (Tokenize)라고 하며, 이 토큰의 값이 임베딩 테이블에서의 값을 가져오기 위한 고유 번호로 볼수 있다. 이렇게 변환된 토큰을 임베딩테이블을 거치면, 4x5 행렬이 나타나며, 이 값이 Token Embedding 값이다. Vaswani의 PE는 삼각함수를 사용하여 포지션을 "Encoding"하였다. 위의 식을 따르면, Position 0번인 단어에 대해서 짝수 차원에는 sin의 값을, 홀수 차원에는 cos의 값을 주게된다. 아래 그림처름 "i love cat" 이라는 문장에서, I에 해당 하는 값은, 첫번째 sin graph에서 0번째, 두번째 cos graph에서 0번째, 3번째 sin graph에서 0번째를 가져와서 만들게 된다. 이렇게 나온 PE는 히트맵으로표현하면 아래와 같다. 조금 더 긴 문장과, 임베딩의 차원을 늘리면 아래와 같다. 이렇게 생성된 값은 앞에 구해진 Token 임베딩과 더해져서 트렌스포머 아키텍처의 초기 Input값으로 사용된다. 파이토치의 구현 코드는 다음과 같이 사용할수 있다. [4] 이런 PE를 Sinusoidal Positional Encoding 또는 Absolute Positional Embedding등 다양하지만, 보편적으로 보는 Positional Embedding / Encoding은 위와 같은 Vaswani의 Sinusoidal Positional Encoding을 의미한다. 이 PE는 구현이 쉽고 가장 베이직한 방법이기에 많이 사용되지만, 각 단어의 위치를 Independent하게 보기때문에 단어간의 관계를 고려하지 않는다. 각 단어의 거리와 관계를 고려하여 트렌스포머를 활용한 연구는 "Relative Positional Embedding"(Shaw et al. https://arxiv.org/abs/1803.02155) 으로 다음글에 리뷰를 진행해보겠다.
-
AWS EKS에서 Fargate 노드 기반 비동기 워크플로 아키텍처 구성하기
EKS 클러스터에서는 AWS의 서버리스 컴퓨팅 엔진인 Fargate를 노드로 사용할 수 있습니다. Fargate를 노드로 사용하면 필요할 때만 노드를 띄워 비용을 절감할 수 있습니다. 이 글에선 Kubernetes Job을 통해 워크플로우를 구성하며 AWS SQS 및 KEDA를 오토스케일러로 사용합니다. EKS 및 SQS는 구성되어있다고 가정합니다 1. KEDA Operator에서 사용할 ServiceAccount 객체 생성 KEDA가 SQS 메시지 대기열을 폴링하기위한 IAM 정책을 작성한 json파일을 생성합니다. + 최소 권한 원칙을 위해 Resource 항목에는 사용할 SQS ARN을 명시합니다 AWS CLI로 통해 작성한 json파일을 기반으로 IAM 정책을 생성합니다. eksctl로 EKS에 생성한 정책을 연결한 역할을 가진 ServiceAccount를 생성합니다 위 명령어 실행 시 AWS CloudFormation 스택에서 리소스를 생성합니다. 위에서 생성한 IAM 정책을 기반으로 IAM 역할을 만들고, EKS 내에 ServiceAccount 객체를 지정한 네임스페이스 내에 생성합니다. IAM 역할 및 ServiceAccount가 잘 생성되었는지 확인해봅니다 2. KEDA helm 차트 배포 Deployment CPU Memory Admission Webhooks Limit: 1, Request: 100m Limit: 1000Mi, Request: 100Mi Metrics Server Limit: 1, Request: 100m Limit: 1000Mi, Request: 100Mi Operator Limit: 1, Request: 100m Limit: 1000Mi, Request: 100Mi KEDA 설치 시 위 3개의 deployment가 배포되며 각 Pod의 리소스 요구사항입니다. KEDA Helm Repository를 추가합니다 $ helm repo update $ kubectl create namespace keda $ kubectl get pods -n keda 3. KEDA Autoscaler 생성 SQS 메시지 대기열을 폴링하며 Kubernetes Job을 오토스케일링하는 ScaledJob 객체를 생성합니다. https://keda.sh/docs/2.12/concepts/scaling-jobs/ Queue Length Max Replica Count Target Average Value Running Job Count Number of the Scale 10 3 1 0 3 10 3 2 0 3 10 3 1 1 2 10 100 1 0 10 4 3 5 0 1 $ kubectl apply -f <작성한 ScaledJob 메니페스트 YAML>


전체댓글0